Weekly Gauge 30: Pricing ve-Boost on Secondary Markets

Part 2: Optimizing supply to maximize price

In our previous article, on understanding the boosting mechanisms subsequent to ve-governance tokens, we’ve briefly introduced a theory on sequential games efficiency also known as Stackelberg game. 

However, in order to not dive too quickly into the deepest pit of the theoretical interpretation of ve-models, we must dedicate this, Part-2, to a more primary concept that differentiates itself from the Stackelberg game by the fact that players act simultaneously, and not in a sequential order, the Cournot Competition.

To put this theory in perspective with the underlying topic, we will define Players as veToken holders who are setting up quantities (locking tokens) simultaneously. In this situation, the price of a veBoost that is going to be set by the market does not depend on the identities of the players but rather the total quantities of the veCRV circulating.

According to this reasoning, it is possible to define the inputs and outputs of the game as : 

• Quantities q1 + q2 = Q as inputs

• Price p of a boost as output 

In microeconomic sequences, the most common function to interpret this is : 

p(q) = a - Q for Q < a where a > 0 is a constant that indicates what the borrower that cares the most about boosts is willing to pay, so as the quantity is being increased the price goes down (which corresponds to supply and demand).

It will ultimately be necessary to define the marginal cost for the boost sellers as Ci >= to 0 that corresponds to fees on boost lending interest, so that a seller will afford the same unit cost for the first unit of veBoost and the fiftieth unit of veBoost.

In the game theoretic perspective, each seller will have the objective of maximizing profit, which can be defined by the function : 

p(q)*qi - Ci*qi 

The next step will naturally be to calculate a pricing an Equilibrium strategy : 

• Derive Player 1 lock needs in response to player 2 lock quantity 

• Derive Player 2 lock needs in response to player 1 lock quantity 

• Find a pair of quantities that are mutual best responses 

To derive the locking needs for both players, they will need to compute the required veToken amounts required to reach maximum boost multipliers for every available pool. Of course, this will have to take in account the liquidity provided in each specific pool.

In the case of Curve Finance for example, you can refer to this very well-written explanation by @DeFi_Cheetah [15-19] : 

DeFi Cheetah🐆 ¤🫐🦇🔊🌿 @DeFi_Cheetah

@CurveFinance @Uniswap @WinterSoldierxz @ConvexFinance @StakeDAOHQ @fraxfinance 15. $CRV emission formula is against any monopoly! How? Let's revisit the formula: boost mechanism calculates one's earning weight by taking the smaller amount of two values. People often neglect the 'min' which prevents any $veCRV holder is too dominant to get most $CRV emitted

 

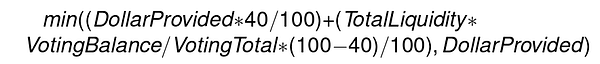
Back to our profit function we can develop it -making sure we distribute the negative signs- to understand how to derive one player best responses to another and the way that they will try to maximize their profit, with the following calculations : 

⇔ p(Q)*q1 - C1*q1 

⇔ (a-Q)*q1 - C1*q1

⇔ (a-(q1+q2)) - C1*q1

⇔ (a*q1) - ((q1)^2) - (q1*q2) - (c1*q1)

Without too many numerical and hypothetical assumptions, we can affirm that the variation of the quantity q1 will draw a bell curve such as a quantity of 0 (null offer) and/or a quantity so high that it will flood the market offer, which will end up with player 1 not making any profit. Again this confirms the balance of supply and demand that we’ve mentioned earlier.

So if we find where the derivative of this function is equal to 0 - which will be the red tangent at the top of the curve-, then we will find where player 1 will be maximizing its profit. This is what we call a First Order Condition : 

⇔ a - (2*q1) - q2 - C1 = 0 

⇔ q1 = (a - q2 - C1) / 2

Basically, this is the point where the marginal cost meets the marginal profit. And we can assume that for any given value that player 2 could choose, player 1's best possible q1 quantity is going to be this point.

This also means that when player 2’s quantity is going up, then the profits available to player 1 are going down because the price will diminish, pushing player 1 to reduce its outputs.

Now that we know how to derive player 1 and player 2 best responses, we can assume there will be an equilibrium where none of them will want to change what they are doing, according to the other player's strategy.

You are now capable to derive an equilibrium between all sellers, representing how much each of them should provide as ve-Boost supply to the market to optimize the price of lending it, that can be represented with the chart below : 

You can observe on this graph that we’ve mentioned Cournot and Stackelberg equilibriums, as well as a perfect competition point, these will be the subject for a future essay on pricing ve-Boost on secondary markets.

We use these approaches to price boosting power on Paladin Warden, a DeFi native product built to enhance ve-Token holders ROI by allowing them to lend their unused boosting power. Currently it has integrated Curve, Balancer, Angle and StakeDAO which represents a total addressable market of 767,930,259$ in TVL. In terms of lendable shares of revenue from those protocols the TAM is 240,968,104$/year.

————

By using our pricing model and given the 4% interest fee taken by Paladin, this would reach a solid 7 figures of annual revenue. Cumulated with the fees generated through the full suite of Paladin products such as Quest -whose TAM on voting incentives average 10M$/year of revenue- and the upcoming ones, the project could earn 8 figures a year with an inflation of its native token that represents a tenth of it in $ value. 

Considering the increasing number of projects implementing ve-tokenomics, the growth potential and scalability for those markets are limitless.

@Beguin